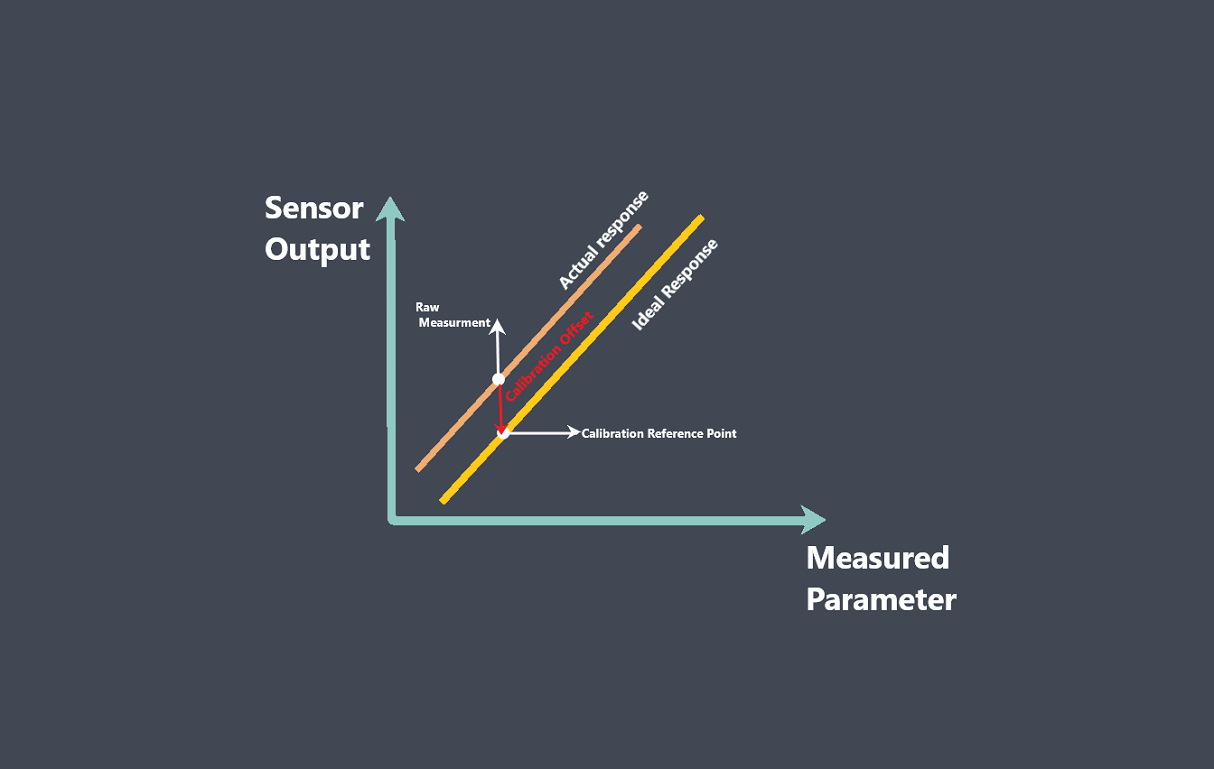
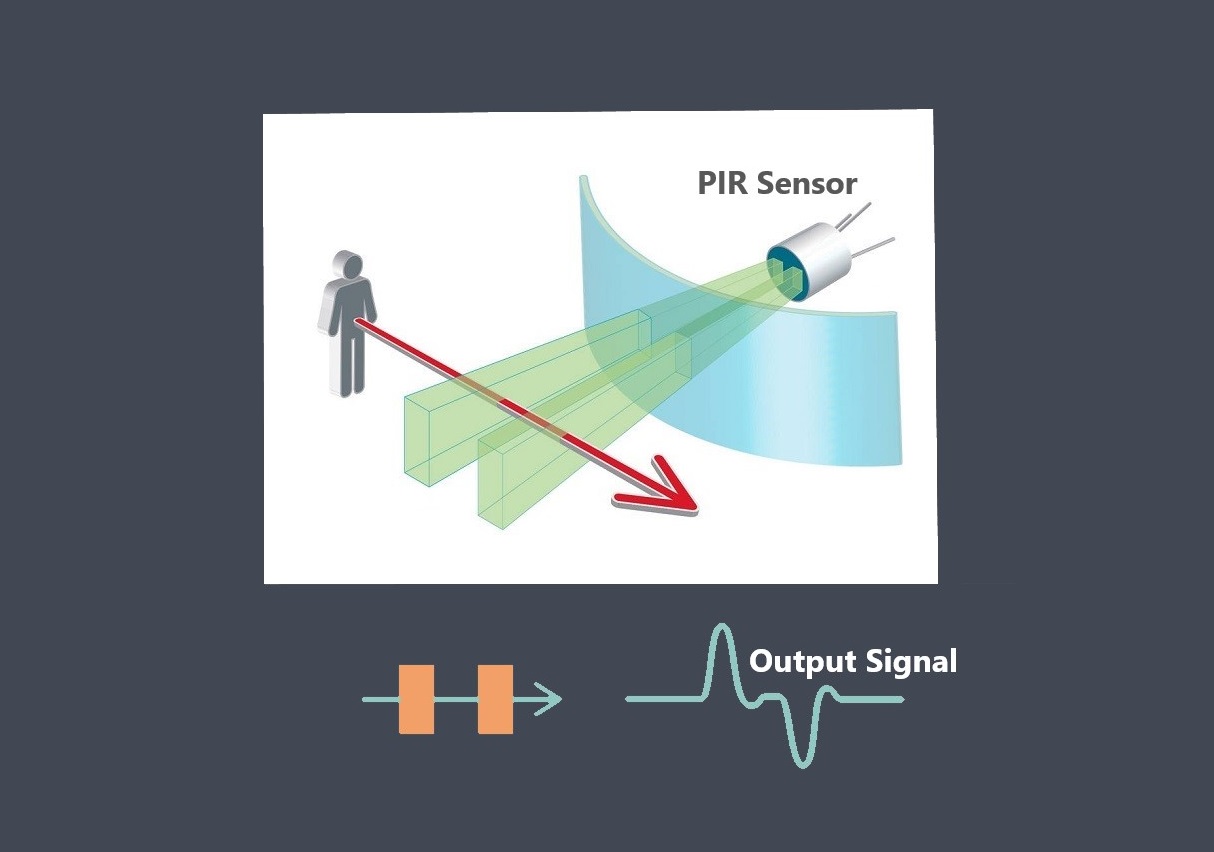
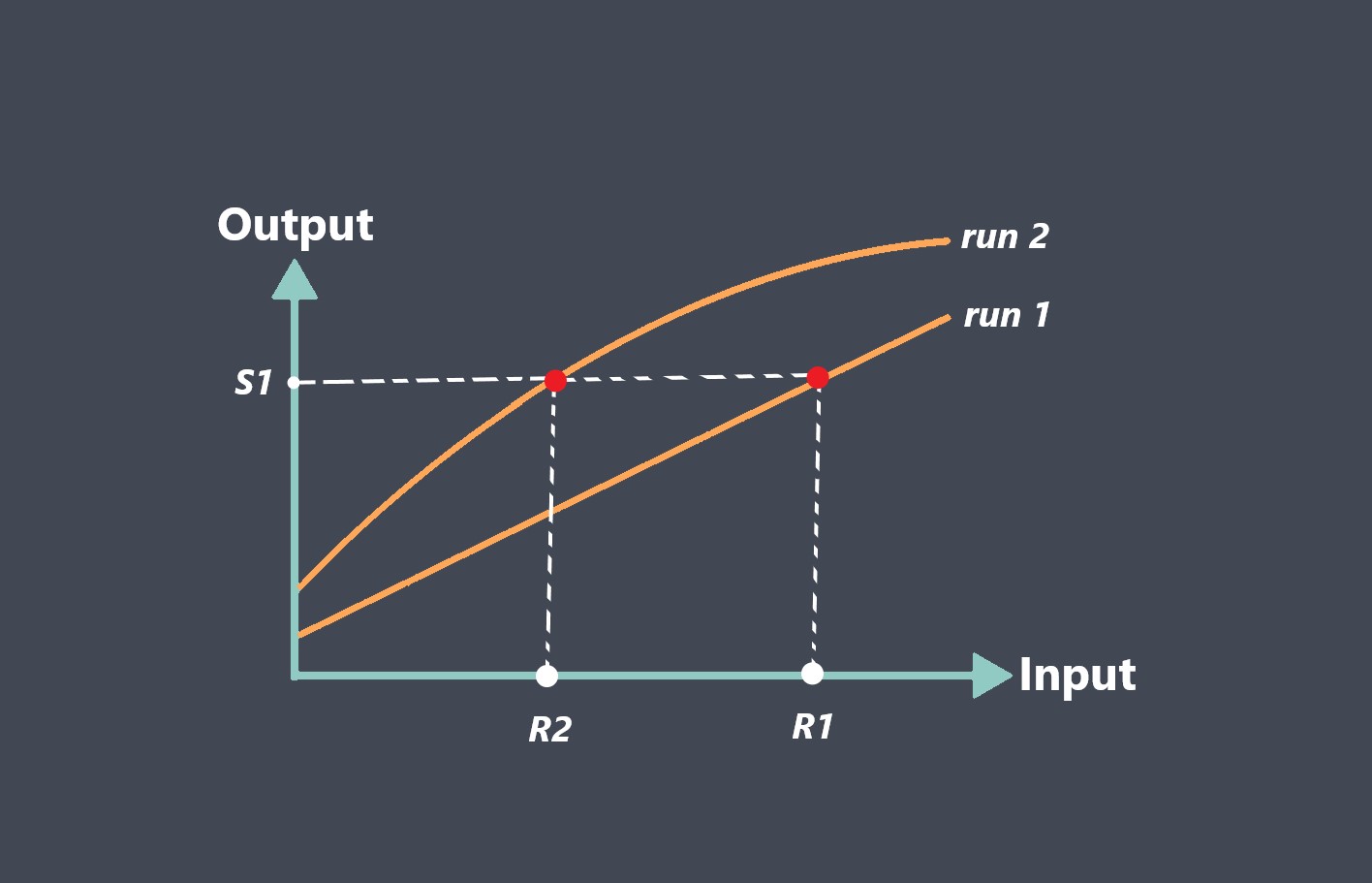
تابع انتقال سنسور یک رابطه ریاضی است که چگونگی تبدیل سیگنال ورودی به سنسور به سیگنال خروجی را توضیح میدهد. این تابع، معادله یا نموداری است که رابطه بین سیگنالهای ورودی و خروجی سنسور را در محدوده مشخصی از ورودیها نشان میدهد.
تابع انتقال یک تابع ریاضی است که نشان دهنده رابطه یک پارامتر اندازه گیری شده فیزیکی است که محرک یا پدیده نیز نامیده می شود. پاسخ سیستم که یک سیگنال خروجی الکتریکی است که رابطه آن را می توان به صورت S = f (p) بیان کرد، که در آن S سیگنال خروجی الکتریکی و p محرک است.
انواع توابع انتقال در زیر آورده شده اند:
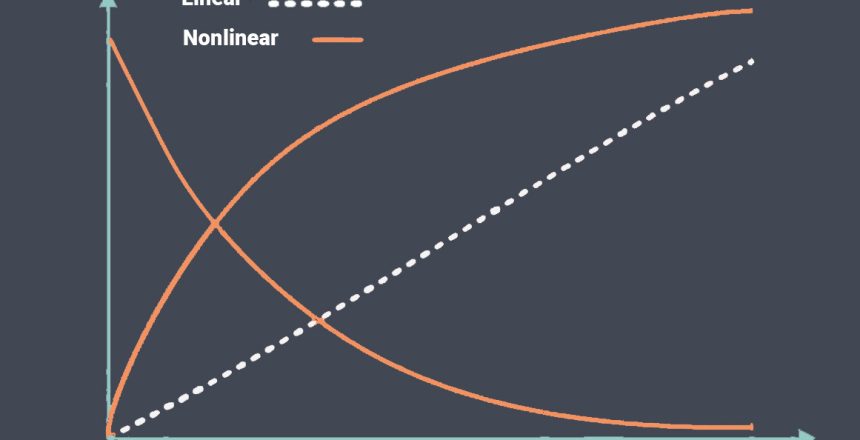
تابع انتقال خطی
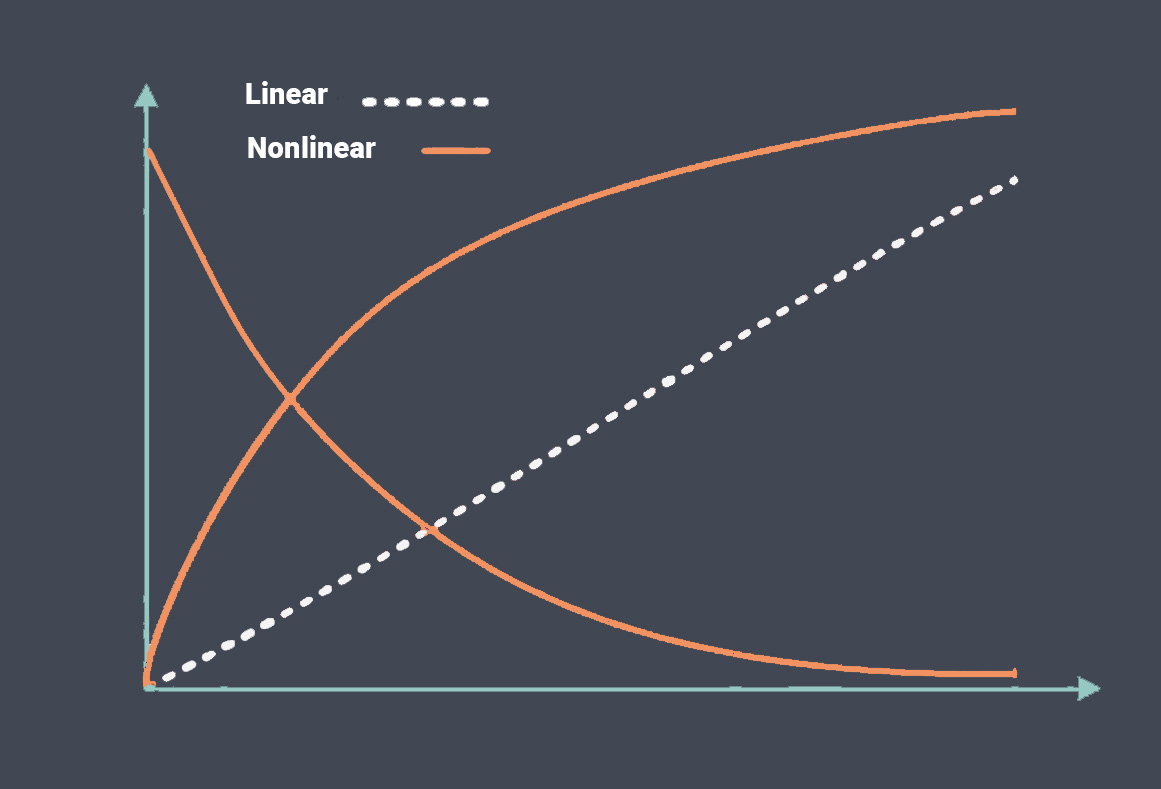
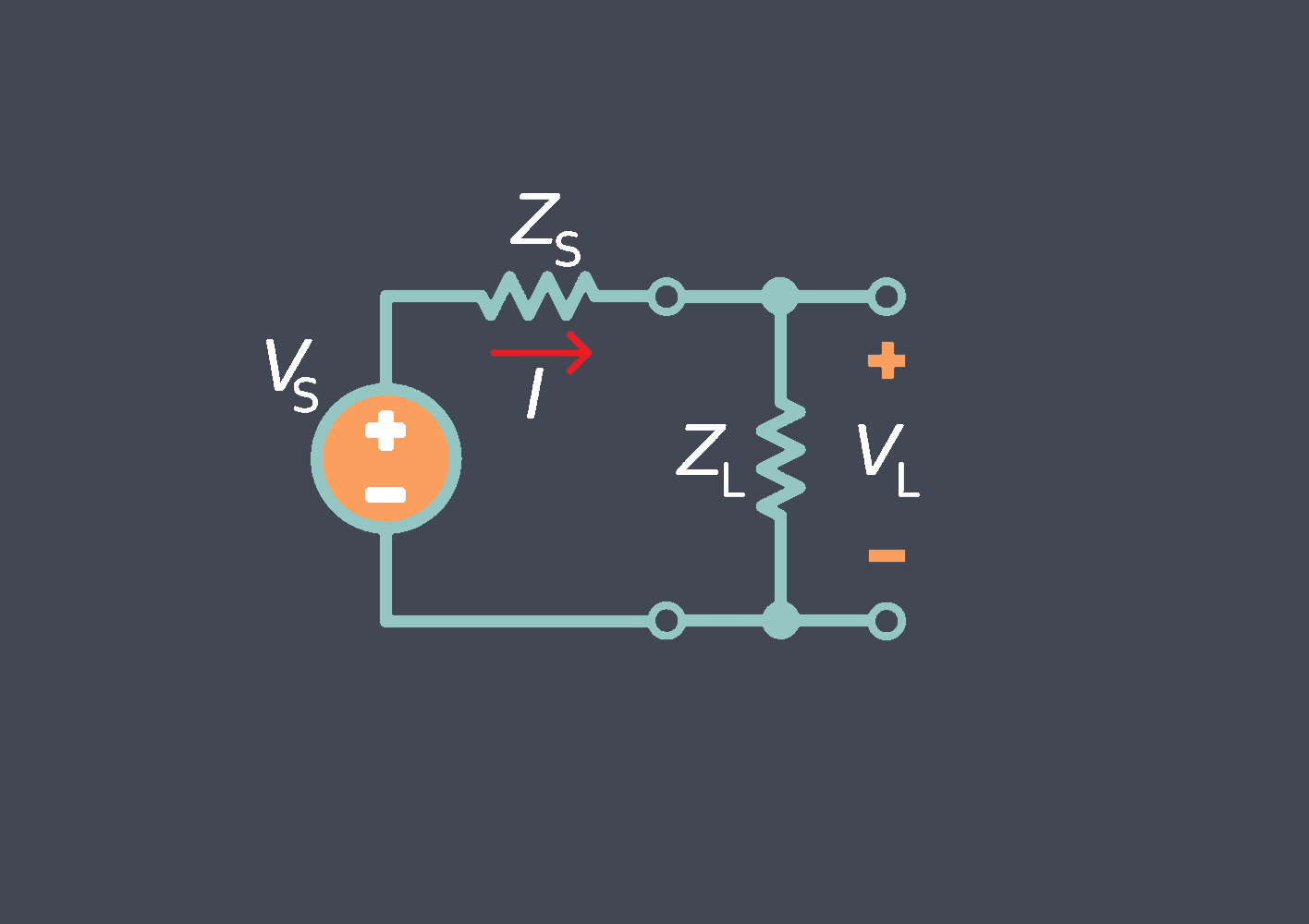
در مهندسی سیستمهای کنترل، یک تابع انتقال خطی، رابطه بین سیگنالهای ورودی و خروجی یک سیستم را در یک سیستم خطی زمان ثابت (LTI) توصیف می کند. معمولاً برای نشان دادن رفتار سیستمهای دینامیکی مانند مدارهای الکتریکی، سیستمهای مکانیکی و فرآیندهای شیمیایی استفاده می شود.
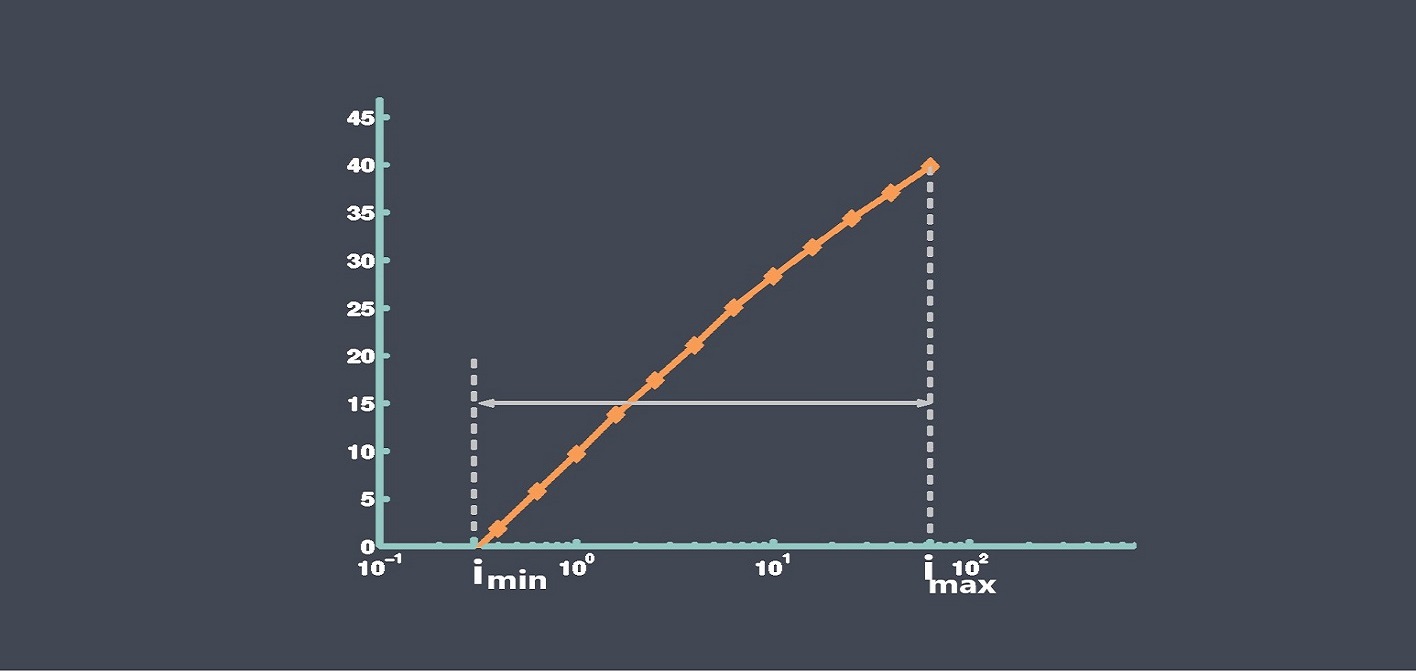
در سنسور خطی، سیگنال خروجی با سیگنال ورودی نسبت مستقیم دارد.
تابع انتقال سنسورهای خطی میتواند به صورت زیر نمایش داده شود:
S= as+b
که در آن

S سیگنال خروجی
s سیگنال ورودی
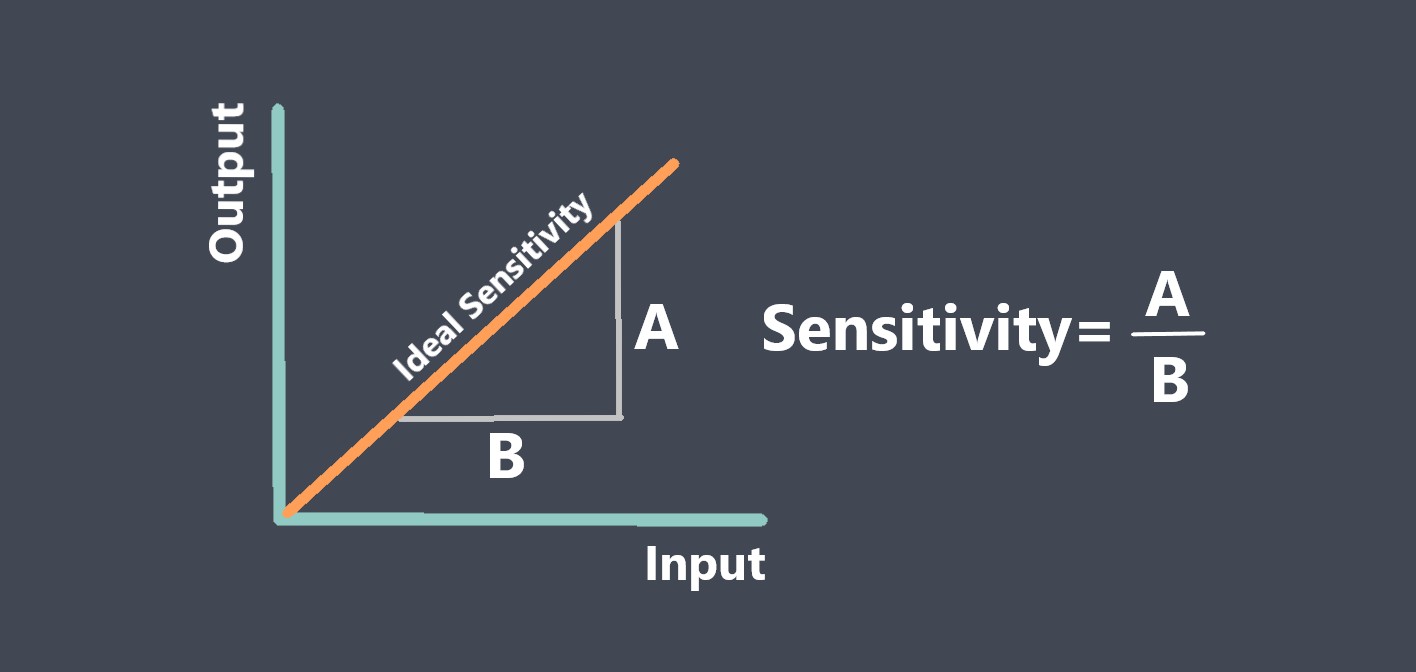
a شیب خط (که گاهی حساسیت نیز نامیده میشود)
b عرض از مبدا
(سیگنال خروجی در سیگنال ورودی صفر)
میباشد
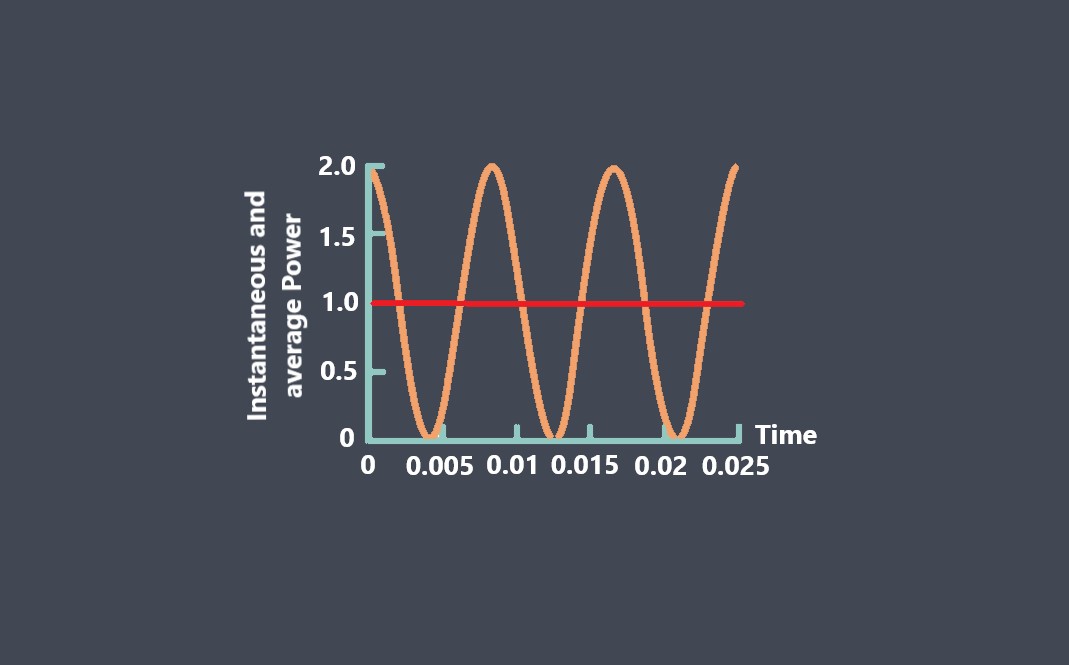
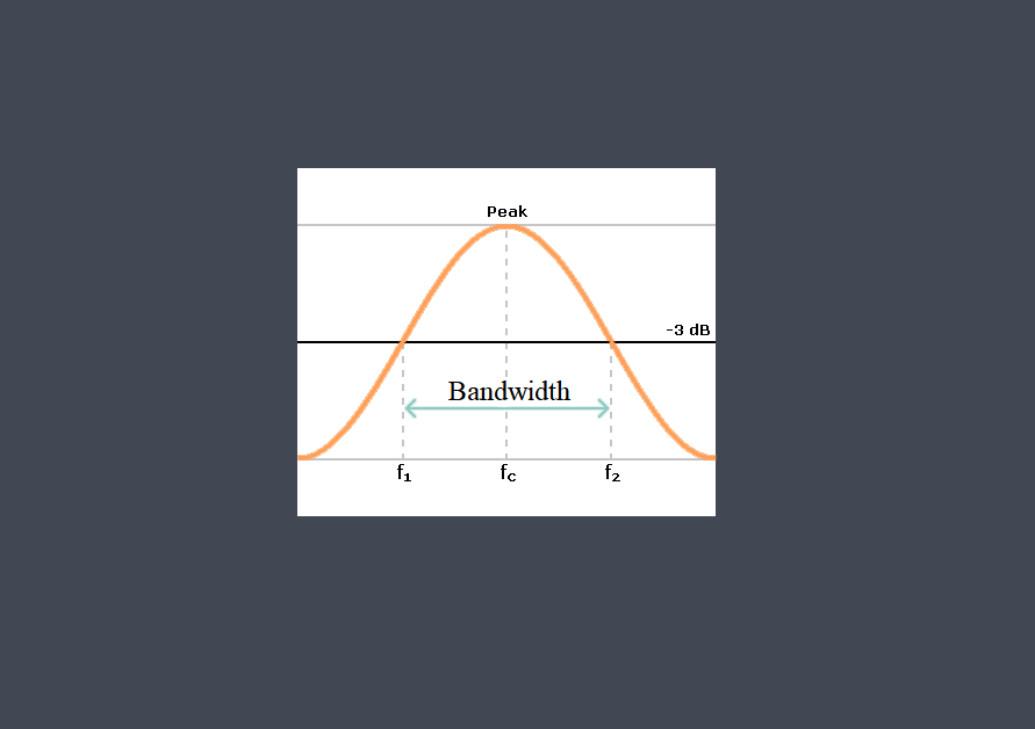
تابع انتقال توضیح میدهد که چگونه سیستم به فرکانسهای مختلف موجود در سیگنال ورودی پاسخ میدهد. دینامیک سیستم، از جمله بهره (تقویت یا تضعیف) و خواص تغییر فاز آن را مشخص میکند.
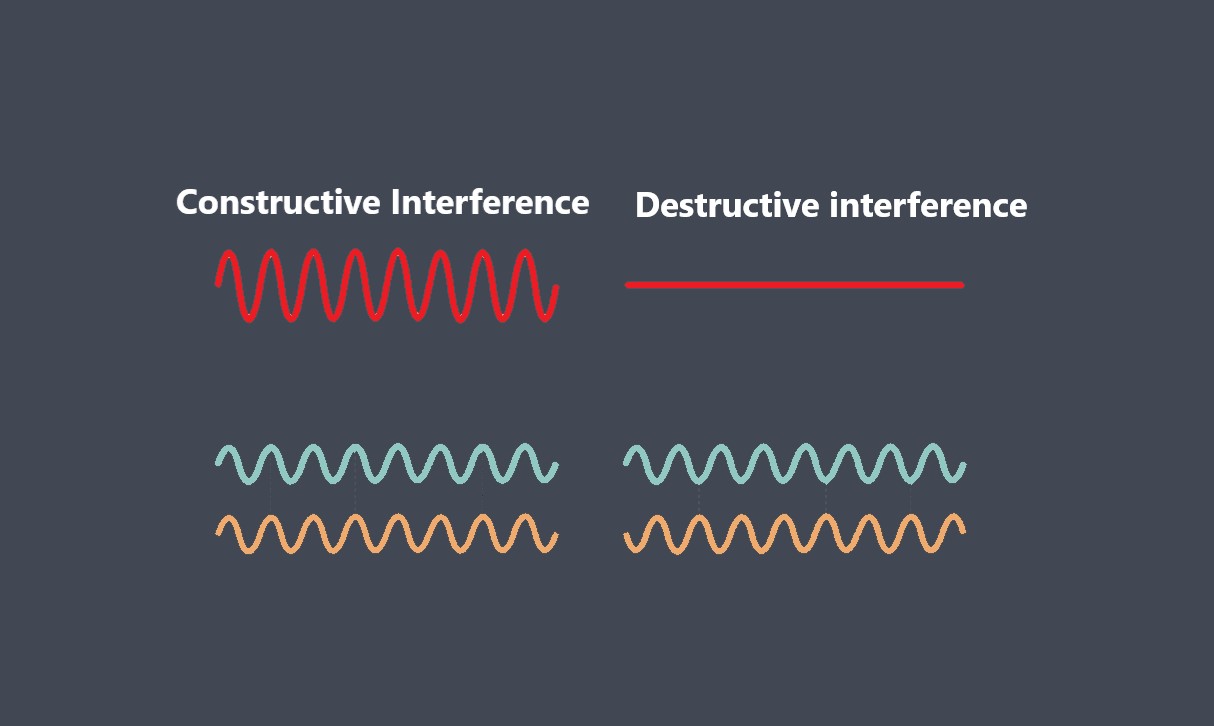
توابع انتقال خطی ویژگی های خطی بودن را برآورده می کنند، به این معنی که از اصول برهم نهی و همگنی پیروی می کنند. برهم نهی بیان می کند که پاسخ به مجموع چندین ورودی برابر است با مجموع پاسخهای جداگانه به هر ورودی. همگنی نیز بیانگر آن است که مقیاس سیگنال ورودی منجر به مقیاس بندی متناظر سیگنال خروجی میشود.
تابع انتقال غیرخطی
تابع انتقال غیرخطی یک رابطه ریاضی است که رفتار ورودی-خروجی یک سیستم یا دستگاه را توصیف می کند که در آن خروجی با ورودی متناسب نیست.
به عبارت دیگر، خروجی از رابطه خطی با ورودی پیروی نمیکند.
بر خلاف توابع انتقال خطی، که میتوانند با یک خط مستقیم یا یک معادله خطی نشان داده شوند، توابع انتقال غیرخطی روابط پیچیده تر و اغلب غیرخطی را بین متغیرهای ورودی و خروجی نشان میدهند.
این روابط میتوانند اشکال مختلفی داشته باشند، مانند توابع نمایی، لگاریتمی، چند جمله ای، مثلثاتی یا تکه ای(چند ضابطه ای) تعریف شده.

درحالت کلی این توابع را میتوان به حالات زیر نوشت:
توابع انتقال لگاریتمی

توابع انتقال نمایی

توابع انتقال توانی

توجه: در تمام معادلات بالا،K یک عدد ثابت است.
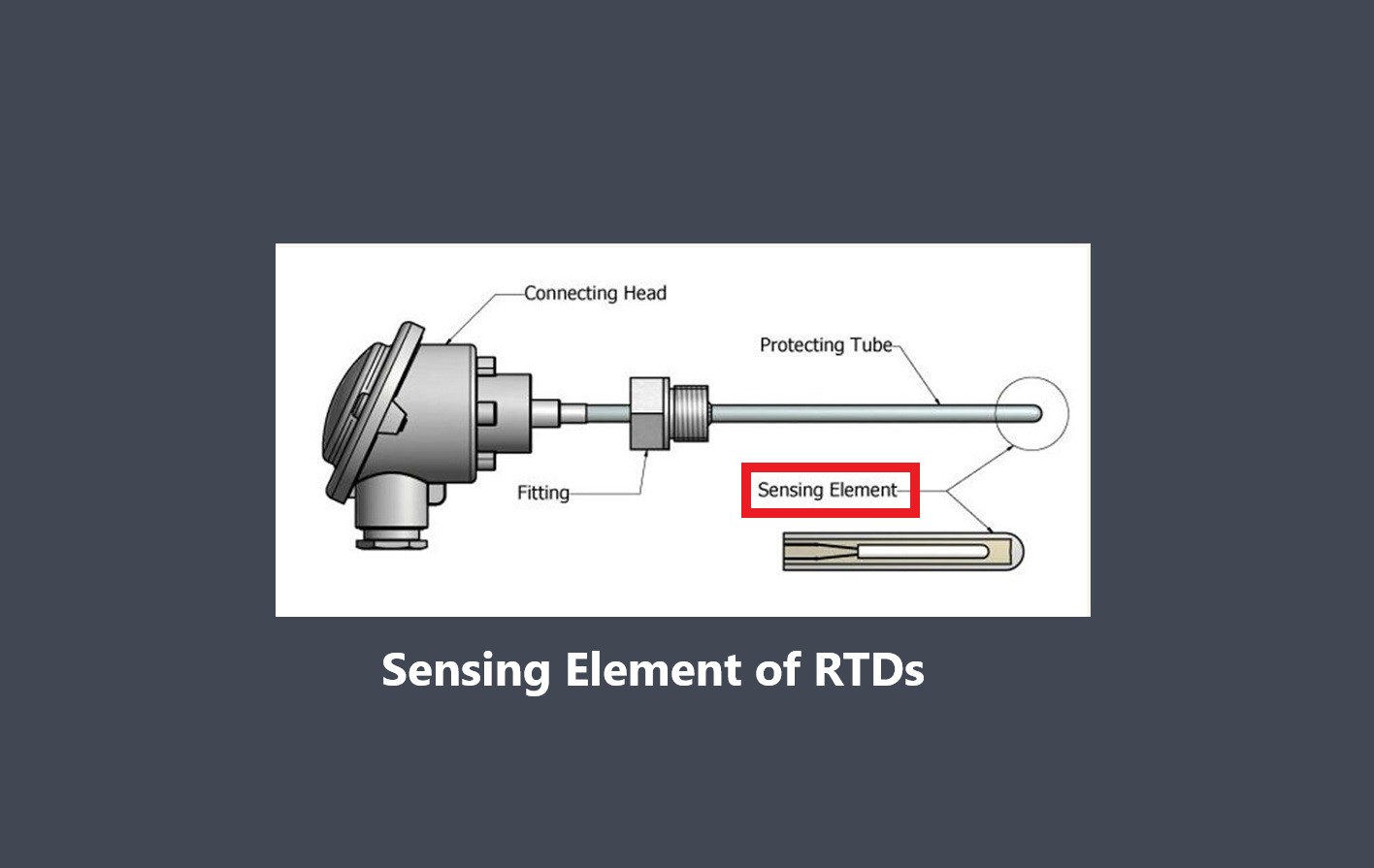
به عنوان مثال، تابع انتقال برای یک ترمیستور، که نوعی سنسور دما، با رابطه غیرخطی بین مقاومت و دما میباشد، می تواند به صورت زیر بیان شود:
R = R0 * exp(B * (1/T – 1/T0))
که در آن
R مقاومت ترمیستور در دمای T ،
R0 مقاومت ترمیستور در دمایT0
B ثابتی که به خواص مواد ترمیستور بستگی دارد
میباشد
نکته: در واقع برای توابع انتقال غیرخطی، بر خلاف رابطه خطی (معادله اول)، شیب خط “m” (ضریب حساسیت) ; عدد ثابتی نیست و برای هر مقدار ورودی خاص X0، می توان آن را به صورت زیر تعریف کرد:

یکی دیگر از ویژگیهای مهم سیستمهای غیرخطی این است که میتوانند طیف وسیعی از پدیدهها را نشان دهند که در سیستمهای خطی وجود ندارند، مانند آشوب، انشعابات و چرخههای حدی. این پدیده ها می توانند به دلیل غیر خطی بودن سیستم به وجود آیند و میتوانند پیامدهای عملی مهمی برای طراحی و کنترل سیستم داشته باشند.
علیرغم پیچیدگی، سیستم های غیر خطی از اهمیت عملی زیادی در بسیاری از زمینههای مهندسی، علم و فناوری برخوردار هستند. به عنوان مثال، سیستمهای کنترل غیر خطی در کاربردهای هوافضا برای کنترل موقعیت و جهت فضاپیماها و در رباتیک برای کنترل حرکت و رفتار روبات ها استفاده میشود. سیستمهای مکانیکی غیر خطی در طراحی وسایل نقلیه و سازهها برای بهبود عملکرد و دوام آنها استفاده میشود. سیستمهای الکتریکی غیر خطی در الکترونیک قدرت برای کنترل جریان نیروی الکتریکی و در سیستمهای انرژی تجدیدپذیر برای تبدیل و ذخیره انرژی از منابع تجدید پذیر استفاده میشود.
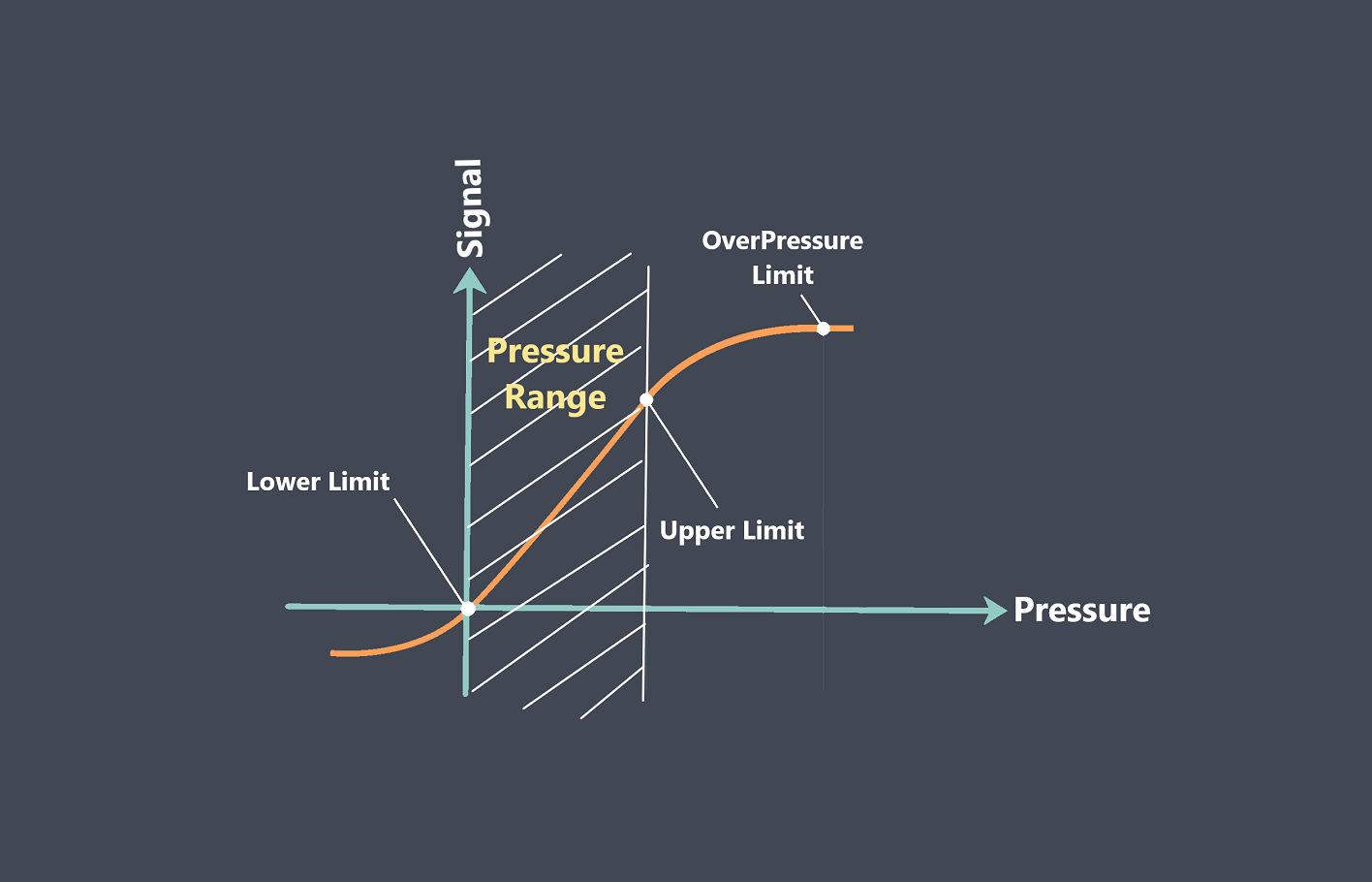
تابع انتقال تکه ای(چند ضابطه ای)
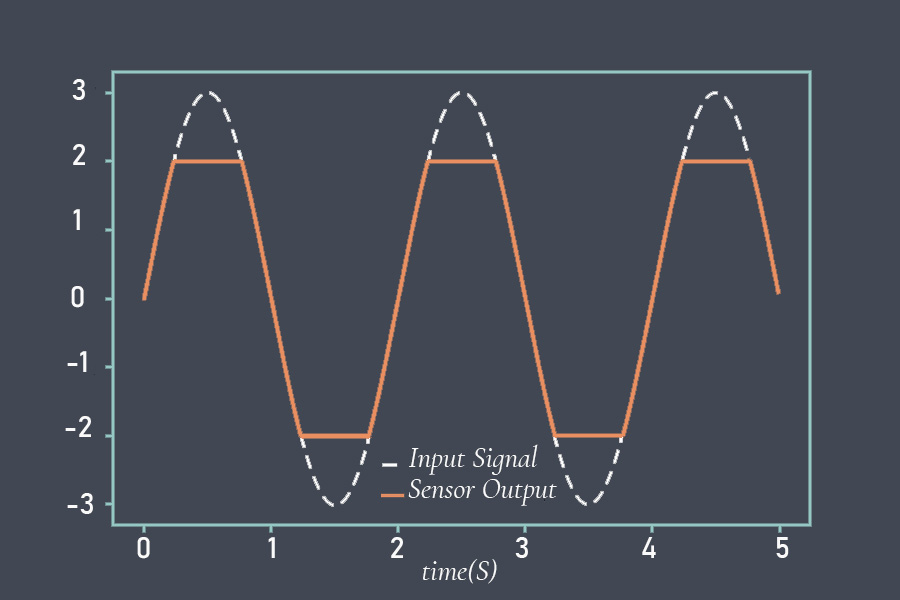
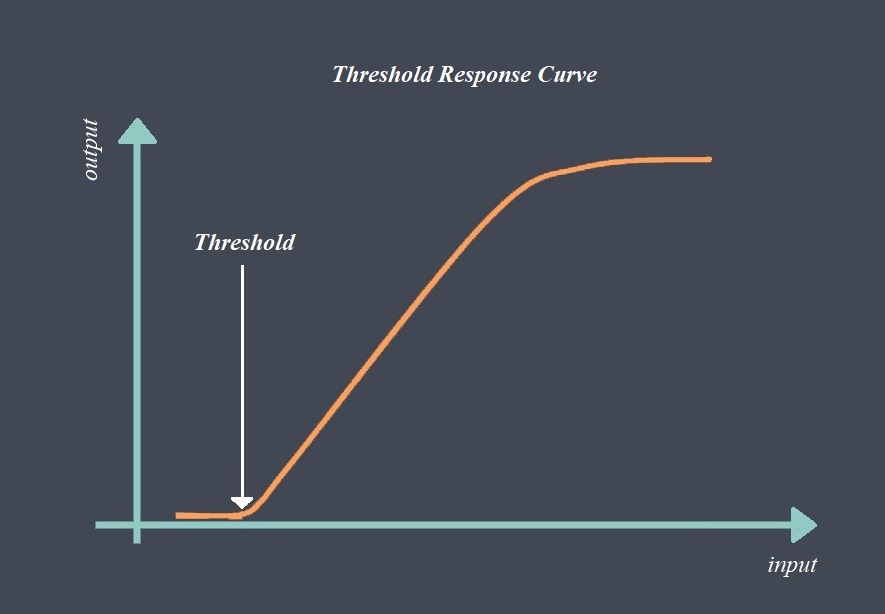
در برخی از سنسورها، تابع انتقال ممکن است تکه تکه باشد، به این معنی که اشکال عملکردی متفاوتی در مناطق مختلف محدوده ورودی دارد. به عبارت دیگر، تابع در نقاط معینی در حوزه ورودی از یک عبارت به عبارت دیگر جابجا میشود و در نتیجه یک تابع به صورت تکه ای تعریف می شود. یک تابع انتقال تکه ای را میتوان به عنوان مجموعهای از معادلات، با معادلات مختلف برای مناطق مختلف محدوده ورودی بیان کرد.
توابع انتقال تکهای معمولاً در سیستمهای کنترل و برنامههای پردازش سیگنال استفاده میشوند، جایی که مدلهای ریاضی مختلف ممکن است برای بخشهای مختلف حوزه ورودی مناسب باشند.
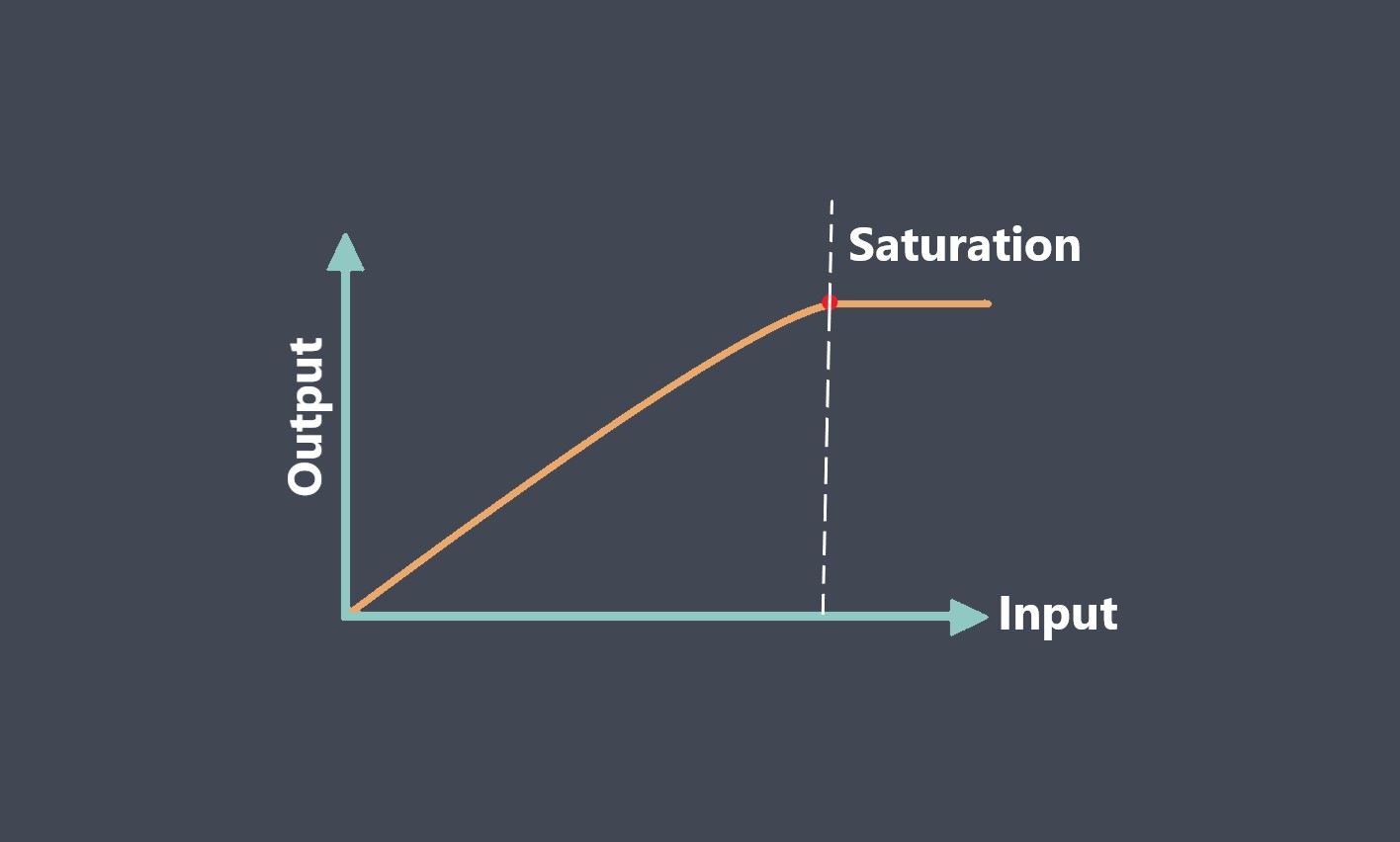
به عنوان مثال، تابع انتقال برای یک لودسل، که نوعی سنسور نیرو است، ممکن است معادلات مختلفی برای مناطق مختلف محدوده بار داشته باشد.
در محدوده low بار، تابع انتقال ممکن است خطی باشد، در حالی که در محدوده high بار، تابع انتقال ممکن است غیرخطی باشد.

تابع انتقال تکه ای را میتوان به صورت مجموعه ای از معادلات برای هر ناحیه از محدوده ورودی بیان کرد.
یک مثال ساده از یک تابع انتقال تکه ای تابع قدر مطلق است که به صورت زیر تعریف می شود:
f(x) = |x| if x < 0
f(x) = x if x >= 0
این تابع یک عبارت ریاضی متفاوت برای x < 0 و x >= 0 دارد که در نتیجه یک تابع به صورت تکه ای تعریف می شود. مثال دیگر تابع “signum” است که علامت ورودی را برمی گرداند:
f(x) = -1 if x < 0
f(x) = 0 if x = 0
f(x) = 1 if x > 0
توابع انتقال تکهای را میتوان با استفاده از تکنیکهایی شبیه به روشهایی که برای انواع دیگر توابع ریاضی مانند ادغام، تمایز و تحلیل فوریه استفاده میشود، تحلیل و دستکاری کرد. با این حال، برای اطمینان از اینکه تابع در نقاط انتقال بین عبارات مختلف ریاضی، پیوسته و قابل تمایز است، باید دقت ویژهای داشت.